Dinamik Programlama (Dynamic Programming) – En Kısa Yol Problemi
14 Aralık 2011
6.810 kez okundu
Yorum yok
(Henüz hiç oy kullanılmadı. İlk oyu siz verin.)
Loading...
(Henüz hiç oy kullanılmadı. İlk oyu siz verin.)Loading...
Arkadaşlar bu yazımda, matematik ve bilgisayar bilimleri alanlarında karmaşık problemleri çözmek için kullanılan bir metoddan bahsedeceğim. Ardından metodla alakalı bir problem olan en kısa yol probleminin çözümünü ve ilgili c kodlarını yazacağım.
Dinamik programlama, karmaşık bir problemi daha alt problemlere bölerek çözmeye çalışan yöntemdir. Bu işlem sırasında elde edilen veriler bir yere kaydedilerek. Daha sonra ihtiyaç olduğunda tekrar hesaplamak yerine buradan kullanılır ve zamandan kazanç elde edilir.
Bir problemi dinamik programlama yöntemiyle çözebilmek için bazı şartlar vardır. Şöyle ki:
- En iyi çözümün alt çözümleri de en iyi olmak zorundadır.
- Var olan karmaşık problemi daha basit ve alt problemlere bölüm, bu alt problemleri çözdükten sonra elde ettiğimiz verilerle büyük problemi çözebilmek.
- Sona gelindiğinde geriye doğru giderek problemi çözmek.
- Her aşamada elde edilen verileri bir noktada saklamak.
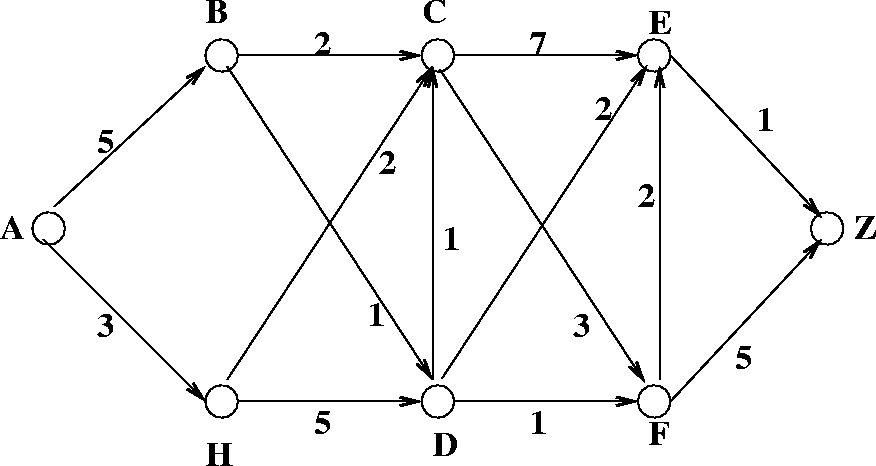
Şimdi örnek bir resim üzerinde problemi anlayalım.
Örneğin yukarıdaki şekilde problem şudur. Bir üretim noktasında iki tane üretim bandı vardır. S1,1 S1,2 …şeklinde devam eden sıra ilk bant, S2,1 S2,2 … şeklinde devam eden sıra ikinci banttır. Ürünümüz enter noktasından bantlara girecek ve exit noktasından çıkacaktır. Amaç en kısa yolu takip etmektir. Kısıtlamalar şöyledir. Örneğin enter noktasıyla S1,1 arasındaki mesafe e1 yani 2 birim dir. Aynı bant üzerinde devam etmek iki noktanın toplamıdır. Yani, S1,1 den S1,2 ye geçerseniz 9 birimlik yol almış olursunuz ve daha önce de 2+7 =9 yol daha aldığınız için toplamda 18 birim yol eder. Ancak 1. banttan ikinci banta atlamak veya tam tersi ekstra yol demektir. Örneğin S1,1 den S2,2 ye geçmek S2,2 den dolayı 5, e1+A1,1 den dolayı 9 ve arada atlama mesafesi olan T1,1 den 2 birim eder ve S2,2 ye gelmek 16 birime mal olur. Bu şekilde hesaplandığına exit noktasına en kısa nasıl gidebiliriz.
Problemin çözümü şu şekilde olacak.Her S noktası için bir önceki iki S noktasının karşışaltırılıp kısa olanın hesaba dahil edilmesi olacaktır. Yani örneğin S1,2 için öncelikle S1,1 =2+7 ve S2,1 = 4+8+2 = 14 değerleri karşılaştırılacak ve S1,2 noktasına en kısa gelen yol olan S1,1 in sonucu S1,2 ye yazılacak. Bu arada S1,2 nin yol maliyeti de eklenecek. Ve ayrı bir noktada her S noktasına hangi banttan gelindiği yazılacak.
Böylece sona vardığımızda okları geriye doğrı takip ederek en kısa yolu bulmuş olacağız.
Bu problemi çözen C kodu şu şekildedir.
Ayrıca dinamik programlamada en çok kullanılan örnek fibonacci serisidir. O problemin anlatımına buradan ulaşabilirsiniz.
Bunlara da Göz Atmak İsteyebilirsiniz.
Rica: Sitemizin Google'da daha üst sıralarda çıkması için lütfen alttaki Google+ veya Begen butonuna tıklayınız , ya da yazılarımızı Facebookta Paylaş butonu ile paylaşabilirsiniz.
Yazılarımızı okuyan okurlarımızın yorumlarını bizimle paylaşmaları, bizi daha çok yazı yazmaya teşvik edecektir. Lütfen yorumlarınızı, görüşlerinizi, eleştirilerinizi bizden esirgemeyin.
<<< Önceki: Csharp ref, out ve params Kullanımı
Sonraki: Kırmızı – Siyah Ağaç Yapıları ( Red – Black Trees) C Kodu >>>
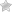
Yorum Bırakın!